Para Ahli Teori Dawai Secara Tidak Sengaja Menemukan Rumus Baru untuk Pi

Sekolahnews – Angka pi (π) muncul di tempat-tempat yang paling tidak mungkin. Angka ini dapat ditemukan di lingkaran , tentu saja—serta di bandul, pegas, dan kelokan sungai. Angka sehari-hari ini dikaitkan dengan misteri transendental . Angka ini telah mengilhami teka-teki pemikiran Shakespeare , tantangan memanggang, dan bahkan sebuah lagu asli . Dan pi terus memberikan kejutan—yang terbaru pada bulan Januari 2024, ketika fisikawan Arnab Priya Saha dan Aninda Sinha dari Institut Sains India menyajikan rumus yang sama sekali baru untuk menghitungnya, yang kemudian mereka terbitkan di Physical Review Letters .
Saha dan Sinha bukanlah ahli matematika. Mereka bahkan tidak mencari persamaan pi yang baru. Sebaliknya, kedua ahli teori string ini sedang mengerjakan teori pemersatu tentang gaya fundamental, yang dapat mendamaikan elektromagnetisme, gravitasi, dan gaya nuklir kuat dan lemah. Dalam teori string, blok dasar penyusun alam semesta bukanlah partikel, seperti elektron atau foton, melainkan benang-benang kecil yang bergetar seperti senar gitar dan dengan demikian menyebabkan semua fenomena yang terlihat. Dalam karya mereka, Saha dan Sinha telah menyelidiki bagaimana senar-senar ini dapat berinteraksi satu sama lain—dan secara tidak sengaja menemukan rumus-rumus baru yang terkait dengan besaran-besaran matematika yang penting.
Selama ribuan tahun, manusia telah mencoba menentukan nilai pasti pi. Hal ini tidak mengherankan, mengingat kegunaan menghitung keliling atau luas lingkaran, yang dimungkinkan oleh pi. Bahkan para ilmuwan kuno mengembangkan pendekatan geometri untuk menghitung nilai ini. Salah satu contoh terkenal adalah Archimedes, yang memperkirakan pi dengan bantuan poligon: dengan menggambar poligon bersisi n di dalam dan satu di luar lingkaran dan menghitung keliling masing-masing, ia mampu mempersempit nilai pi.

Guru sering kali mengajarkan metode ini di sekolah. Namun, meskipun kita tidak mengingatnya, kita mungkin dapat membayangkan bahwa prosesnya cukup rumit. Archimedes bahkan membandingkan keliling poligon dengan 96 titik sudut untuk membuktikan bahwa pi berada di antara 3,1408 dan 3,1429. Oleh karena itu, pendekatan ini tidak terlalu praktis untuk menghitung pi secara tepat.
DERET TANPA BATAS UNTUK MENENTUKAN PI
Pada abad ke-15, para ahli menemukan deret tanpa batas sebagai cara baru untuk menyatakan pi. Dengan menjumlahkan angka-angka satu per satu, nilai pi dapat diperoleh. Dan semakin banyak penjumlahan yang kita lihat, semakin akurat hasilnya.
Misalnya, cendikiawan India Madhava, yang hidup dari tahun 1350 hingga 1425, menemukan bahwa pi sama dengan 4 dikalikan dengan deret yang dimulai dengan angka 1 dan kemudian secara bergantian mengurangi atau menambahkan pecahan di mana angka 1 ditempatkan di atas angka ganjil yang lebih tinggi secara berurutan (jadi 1/3 , 1/5 , dan seterusnya ). Salah satu cara untuk mengungkapkannya adalah :

Rumus ini memungkinkan Anda menentukan nilai pi setepat yang Anda inginkan dengan cara yang sangat sederhana. Anda tidak harus menjadi ahli matematika untuk mengerjakan persamaan ini. Namun, Anda perlu kesabaran. Diperlukan waktu yang lama untuk mendapatkan hasil yang akurat. Bahkan jika Anda mengevaluasi 100 penjumlahan, Anda masih akan jauh dari sasaran.
Seperti yang ditemukan Saha dan Sinha lebih dari 600 tahun kemudian, rumus Madhava hanyalah kasus khusus dari persamaan yang jauh lebih umum untuk menghitung pi. Dalam karya mereka, para ahli teori string menemukan rumus berikut:
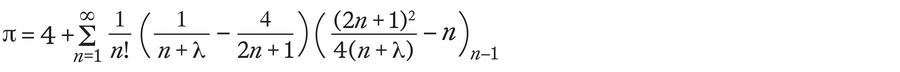
Rumus ini menghasilkan jumlah yang tak terhingga. Yang mengejutkan adalah rumus ini bergantung pada faktor λ, parameter yang dapat dipilih secara bebas. Berapa pun nilai λ, rumus akan selalu menghasilkan pi. Dan karena ada banyak sekali angka yang dapat berkorespondensi dengan λ, Saha dan Sinha telah menemukan rumus pi yang jumlahnya tak terhingga.
Jika λ sangat besar, persamaan tersebut sesuai dengan rumus Madhava. Artinya, karena λ hanya muncul dalam penyebut pecahan, pecahan yang sesuai untuk λ = ∞ menjadi nol (karena pecahan dengan penyebut besar sangat kecil). Untuk λ = ∞, persamaan Saha dan Sinha mengambil bentuk berikut:

Bagian pertama persamaan tersebut sudah mirip dengan rumus Madhava: Anda menjumlahkan pecahan dengan penyebut ganjil. Namun, bagian terakhir dari jumlah (– n ) n – 1 kurang familiar. Subskrip n – 1 adalah yang disebut simbol Pochhammer. Secara umum, ekspresi ( a ) n sesuai dengan produk a x( a + 1) x ( a + 2) x … x ( a + n – 1). Misalnya, (5) 3 = 5 x 6 x 7 = 210. Dan simbol Pochhammer dalam rumus di atas karenanya menghasilkan: (– n ) n – 1 = (– n ) x (– n + 1) x (– n + 2) x … x (– n + n – 3) x (– n + n – 2).
BEBERAPA LANGKAH MENUJU FORMULA MADHAVA
Semua elemen ini terlihat rumit pada awalnya, tetapi dapat disederhanakan dengan cepat. Pertama, kurangi –1 dari setiap faktor. Oleh karena itu, tanda di depan produk besar adalah –1 jika n ganjil dan +1 jika n genap, sehingga Anda memperoleh (– n ) n – 1 = (–1) n x n x ( n – 1) x ( n – 2) x … x ( n – n + 3) x ( n – n + 2). Faktor terakhir dapat disederhanakan lebih lanjut: (– n ) n – 1 = (–1) n x n x ( n – 1) x ( n – 2) x … x 3 x 2 x 1.
Ekspresi yang diperpanjang ini sebenarnya adalah (– n ) n – 1 = (–1) n x n , sehingga menghasilkan bentuk berikut:

Hal ini sesuai dengan rumus Madhava. Persamaan yang ditemukan oleh Saha dan Sinha juga memuat deret yang ditemukan oleh Madhava.
Namun, seperti yang dilaporkan oleh kedua ahli teori string, pi dapat dihitung jauh lebih cepat untuk nilai λ yang lebih kecil. Sementara hasil Madhava membutuhkan 100 suku untuk mendapatkan dalam 0,01 dari pi, rumus Saha dan Sinha untuk λ = 3 hanya membutuhkan empat suku pertama. “Sementara seri [Madhava] membutuhkan 5 miliar suku untuk konvergen ke 10 tempat desimal, representasi baru dengan λ antara 10 [dan] 100 membutuhkan 30 suku,” tulis para penulis dalam makalah mereka. Saha dan Sinha tidak menemukan metode yang paling efisien untuk menghitung pi. Seri lain telah dikenal selama beberapa dekade yang memberikan nilai yang sangat akurat jauh lebih cepat. Yang benar-benar mengejutkan dalam kasus ini adalah bahwa fisikawan muncul dengan rumus pi baru ketika makalah mereka bertujuan untuk menggambarkan interaksi string. Mereka mengembangkan metode untuk menunjukkan probabilitas dengan mana dua string tertutup akan berinteraksi satu sama lain—sesuatu yang telah dicari oleh banyak ahli teori string selama beberapa dekade tanpa hasil.
Ketika Saha dan Sinha mencermati lebih dekat persamaan yang dihasilkan, mereka menyadari bahwa mereka dapat mengekspresikan angka pi dengan cara ini, serta fungsi zeta, yang merupakan inti dari dugaan Riemann , salah satu misteri terbesar yang belum terpecahkan dalam matematika. Mengingat minat para ahli teori string, rumus mereka untuk pi dan fungsi zeta hanya menghiasi paragraf terakhir dari makalah mereka. “Motivasi kami, tentu saja, bukanlah untuk menemukan rumus untuk pi,” kata Sinha dalam video YouTube dari Numberphile . “Pi hanyalah produk sampingan.”
(sumber:scientificamerican.com)
